Home

Lab tour

Tutorial

QuanTechi

In the media

← The institute

← Physics in Calgary

Quantum states containing a definite number of energy quanta (Fock states) play a key role in quantum optics. They constitute the essence of the quantum nature of light and are indispensable in the theoretical description of a wide range of optical phenomena. Fock states also play a major role in more applied aspects of quantum optics, such as the rapidly developing fields of quantum communication and information. Of particular importance is their application in quantum cryptography which would result in a significant increase in capacity and security of communication channels. Superpositions of the vacuum and the single-photon state in a certain optical mode can also be used to implement a qubit.

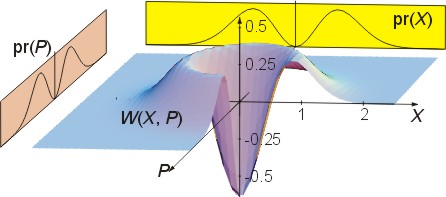
Despite their importance, pure number states are extremely rare in nature [W. E. Lamb in his paper “Anti-photon” writes: “There is no such thing as a photon. Only a comedy of errors and historical incidents led to its popularity among physicists and optical scientists”], and their synthesis in a laboratory constitutes a rather involved task. Perhaps this is the main reason this state has not been investigated and characterized so far. Our intention was to fill this gap: to generate the single-photon Fock state and to characterize it by means of homodyne tomography. Our second motivation for undertaking this experiment was the fact that the state’s “quantum portrait” – its Wigner function – shows strongly non-classical features by exhibiting large negative values in certain regions of the phase space [Fig. 1]. The only non-classical state of light investigated previously was the squeezed state whose Wigner function is positive definite and all marginal distributions are Gaussian.

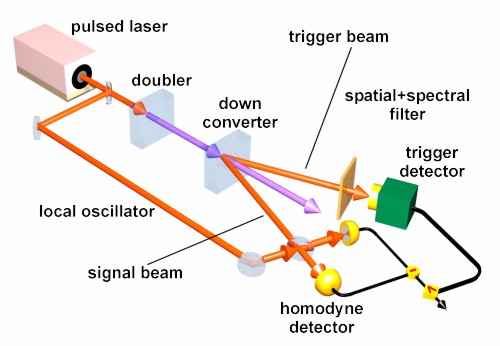Several groups around the world are working on a “photon pistol” – a device which would generate a single photon when classically triggered – but none of the approaches attempted so far have fully resolved this task. To succeed in our experimental work we had to use an alternative approach: prepare single photons by conditional measurements on a biphoton state generated by means of parametric down-conversion (PDC) [Fig.2]. In PDC, a “pump” photon propagating through a nonlinear crystal may spontaneously annihilate to produce two photons of lower energy in the form of a highly entangled quantum state known as biphoton. The two generated photons are separated into two emission channels. Detection of a photon in one of the emission channels (labeled trigger) causes the non-local photon pair to collapse projecting the quantum state in the remaining (signal) channel into a single-photon state.

One should understand that the picture above is a great oversimplification, There is no trigger and signal beams in the traditional sense. The biphoton – the entangled state emitted by the down-converter is a very complex entity and is emitted into a wide solid angle. The optical mode of the signal state is created non-locally only when a photon of a pair hits the trigger detector and is registered. The coherence properties of this mode are determined by the optical mode of the pump and the spatial and spectral filtering in the trigger channel.

Homodyne tomography requires that the mode be matched (spatially and temporally) with that of the local oscillator. Since in our case the signal mode is extremely weak (only one photon!) and ”virtual” (i.e. created non-locally), achieving this mode matching was a major challenge. First, we needed to prepare our photon in a well-defined spatiotemporal mode. Second, we need to make sure this mode is identical to that of the local oscillator. More details on how we have achieved this can be found in this paper.

Another challenge we faced in setting up the experiment was the technical requirements to the balanced homodyne detector. Since all measurements were performed in the pulsed regime (it is much easier to define a single-photon pulse than a single-photon continuous wave), our detector had to resolve quantum shot noise of individual laser pulses. This means that it must exhibit low electronic noise and a flat amplification profile in a wide RF range between DC and ~ 1 MHz. This is very different from the traditional frequency-domain homodyning technique used to investigate squeezed light, in which only a certain frequency component (normally around 5-10 MHz) of the 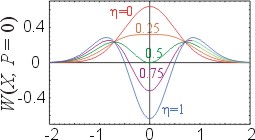difference photocurrent is analyzed to characterize the state of light. See this paper for detais.

In a real experiment the state measured with the homodyne detector is not an ideal Fock state |1> but a statistical mixture whose density matrix can be approximated as ρ_meas = η|1><1| + (1-η) |0><0|. The quantity η is the measurement efficiency which is the probability that whenever a photon is observed with the trigger photodiode, its counterpart photon will reach the homodyne detector within the spatio-temporal mode of the local oscillator. This is the main indicator of the quality of our experiment: for η = 1 we get a pure Fock state, for η=0 – a vacuum state. The greater η, the deeper the dip in the Wigner function [Fig. 3]; classically impossible negative values are obtained when η>0.5. For our setup [Fig. 4], the efficiency is about 60% so the Wigner function does become negative at the origin of the phase space.

The measurement efficiency depends on many factors: optical transmission of the signal photon, quantum efficiency of the homodyne detector, trigger dark counts, optical mode matching of the signal photon and the local oscillator, spatiotemporal coherence of the signal photon. The latter factor is very crucial as it is strongly dependent on the spatial and frequency selection in the trigger channel. To obtain a clean coherent mode that can be matched to that of the local oscillator filtering needs to be very tight, which, in turn, results in relatively low trigger count and data acquisition rates.

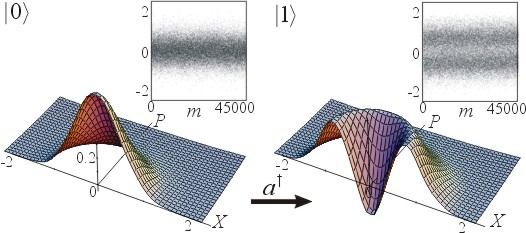Fig. 4 shows our experimental results: 45000 quantum quadrature noise samples acquired for the vacuum and “Fock” (η = 60 %) states. Since both these states carry no phase information, there is no need to acquire several marginal distributions associated with different phases. We just assume that our marginal distributions are all the same and reconstruct the Wigner function. As expected, it turns out to be negative around the origin of the phase space.

Why is this result so amazing? The technique of homodyne tomography can be fully understood in the framework of classical physics. In other words, our experiment could have been conducted (and interpreted) by someone who does not believe in quantum mechanics. Yet the result (s)he would obtain would be completely absurd, incompatible with his or her picture of the world. Imagine that a doctor investigating a patient’s head via the technique of computer tomography and discovering that there is a region inside the head where there is not just nothing, but less than nothing! Our result is completely incompatible with classical physics – thus serving as a very strong evidence of quantum mechanics.

How does quantum mechanics help us to deal with this “absurd” result? In the quantum world, the notion of a “certain point in the phase space” does not make sense because the position and the momentum cannot be measured simultaneously (Heisenberg's uncertainty principle). Neither does the phase-space probability distribution. The Wigner function is not a probability density (only its marginal distributions are) and therefore it is sometimes allowed to be negative.

Our paper on this experiment: Physical Review Letters 87, 050402 (2001)

A paper in which we show that even if the efficiency is less than 50 %, our ensemble is still non-classical: Physical Review A 65, 033830 (2002)

Click here for a popular description of the work in Physical Review Focus

Click here for our own exercise in popularizing the experiment